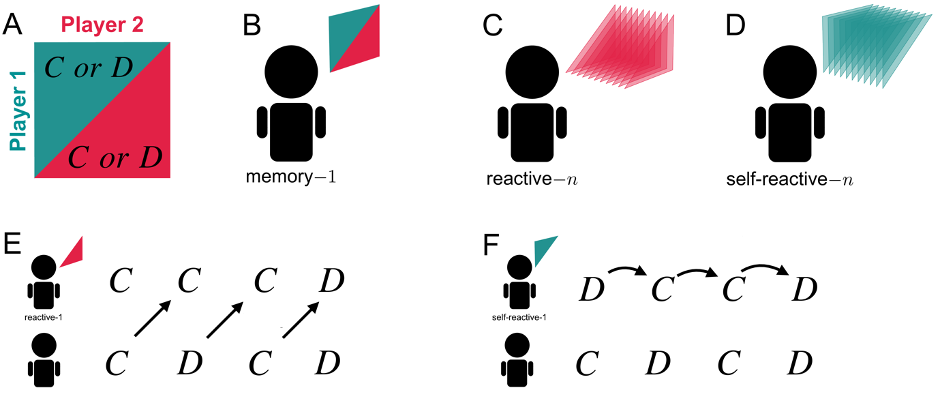
Strategies in repeated games vary widely in complexity. A common way to quantify a strategy's complexity is by the amount of memory it uses, ranging from memory-0 strategies, which disregard prior rounds, to memory-1 strategies, which consider only the most recent interaction, to strategies with more than 1 round memory. Despite their simplicity, memory-1 strategies have historically dominated theoretical studies of reciprocity. However, recent research suggests that human decision-making often incorporates longer memory, particularly in noisy environments where unintended errors occur. This raises important questions: how can longer-memory strategies be analyzed, and what are their implications for understanding cooperation?
Reactive-n strategies
To analyze longer-memory strategies, our new study focuses on a more interpretable set called reactive-n strategies. These strategies rely solely on the co-player's actions during the last n rounds. We show that within the space of reactive-\(n\) strategies, it is possible to explicitly characterize all Nash equilibria. This breakthrough stems from a key insight: if one player adopts a reactive-\(n\) strategy, the other can always find an optimal response among self-reactive-\(n\) strategies, which depend only on the player's own previous \(n\) actions.
This simplification enables a full characterization of partner strategies, Nash equilibria that sustain full cooperation, for memory lengths \(n=2\) and \(n=3\).
We extend our results to counting strategies, a subset of reactive-\(n\) strategies that respond to the total number of times the co-player has cooperated in the last \(n\) rounds, disregarding the sequence of actions. For a specific game called the donation game, our results provide a general characterization of partner strategies for any \(n\). The conditions are surprisingly simple: for every defection by the co-player within memory, the focal player's cooperation rate decreases proportionally by \(c/(nb)\), where \(c\) and \(b\) are the cost and benefit of cooperation.
To evaluate the relevance of partner strategies for the evolution of cooperation, we conduct extensive simulations for three different strategy classes: the classes of reactive-1, reactive-2, and reactive-3 strategies. The results indicate that evolution strongly favors partner strategies and that these strategies are crucial for fostering cooperation. Moreover, we show that as memory length increases, partner strategies are favored more, allowing for greater stability in cooperative behavior. In contrast, for counting strategies, any positive effect of increasing memory is significantly dampened.
Overall, our research highlights the critical role of memory in fostering cooperation. It offers a pathway to reinterpret existing findings and deepen the understanding of reciprocity dynamics.
The article is now available online: https://www.pnas.org/doi/10.1073/pnas.2420125121. You can also download a copy here: https://nikoleta-v3.github.io/publications/Glynatsi2024PNAS.pdf.